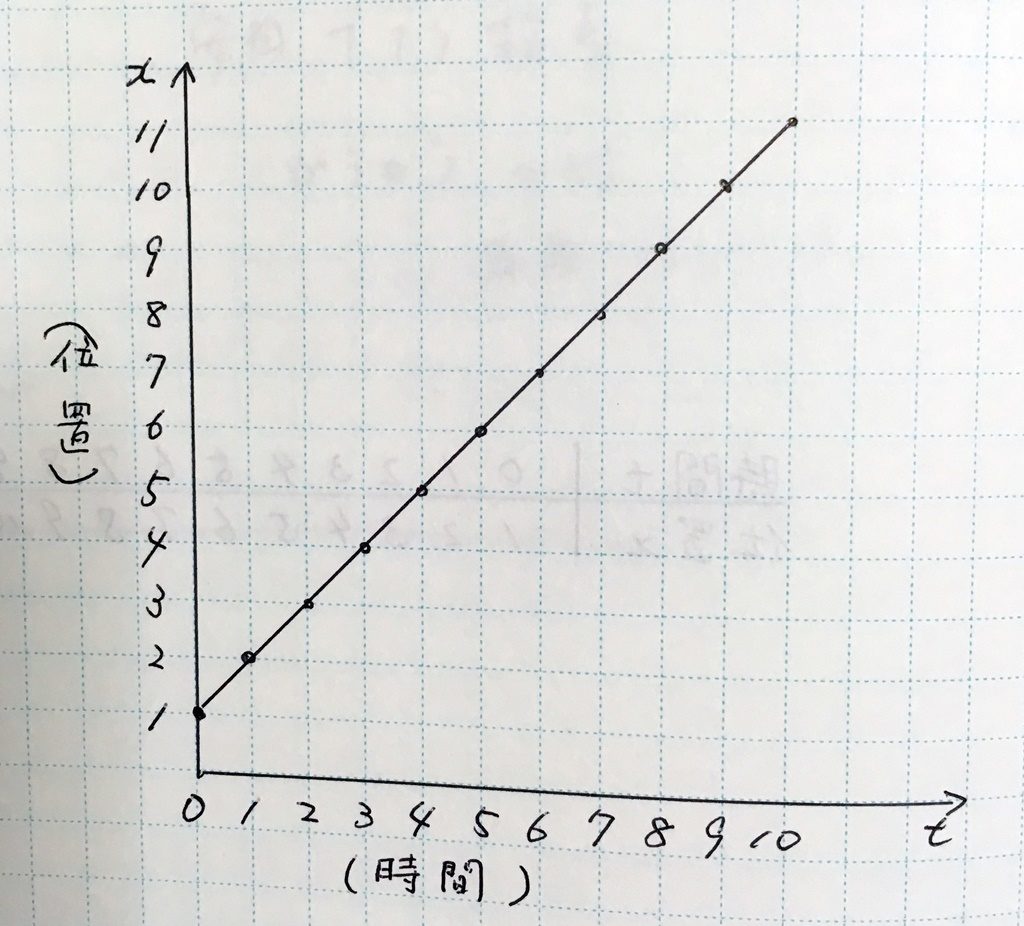ここからの時間は、ゆーき先生が欅坂46平手友梨奈ちゃんをイメージした架空のキャラクターてちこちゃんに相対性理論を教える教室。前回はモヤモヤを解消するはずが、逆に疲れてきた感じがするけども……強力な助っ人が登場するらしいぞ! では今日もゆーき先生の相対LOCKS!

生徒の皆さんこんばんは、相対LOCKS担当のてちこです。前回は、沢山グラフを書いたような気がします……
ガラガラ(扉の開く音)

今日は沢山数式が出てきます

えーっ、そんなー、もう無理ですって

その前に挨拶ね

あ……こんばんは

こんばんは。まあ式自体はそんなに難しいわけではないんだけど、今日は特別ゲストを呼びましたから。では、どうぞ!

こんばんはー

え? ちょっと、なんで?

では、自己紹介をお願いします

神奈川県出身、欅坂46の尾関梨香ちゃんをイメージしたキャラクター、おぜです

おぜちゃんよろしくね

え? なんでおぜなの? ジェットコースターに乗ったから?

え? 何の話?

“SCHOOL OF LOCK!”の裏番ぐ……じゃなかった同時間帯に放送でおなじみの文化放送”オテンキのりのレコメン!”で以前尾関梨香ちゃんがゲスト出演した時に、「数学とか得意」と話してたのでご登場いただきました
⏰この後11:45頃~
実録・レコメン!リスナー事件簿!今夜は欅坂46の菅井友香ちゃん、織田奈那ちゃん、尾関梨香ちゃんが事件の真相に迫る‼️あなたの周りで起こった事件を募集中📬➡️reco@joqr.net
🎁採用された人には、
オリジナル手帳📙をプレゼント!#reco1134 #欅坂46 pic.twitter.com/sMHxHrrpq9— レコメン! (@reco_oshirase) 2018年8月13日
(ちなみに、ここに写っている緑の服の女性が本物の尾関梨香さんです)

えーっ、なんか意外

ちょっと! もう、きょうは任せなさい!

では本題に入るよ
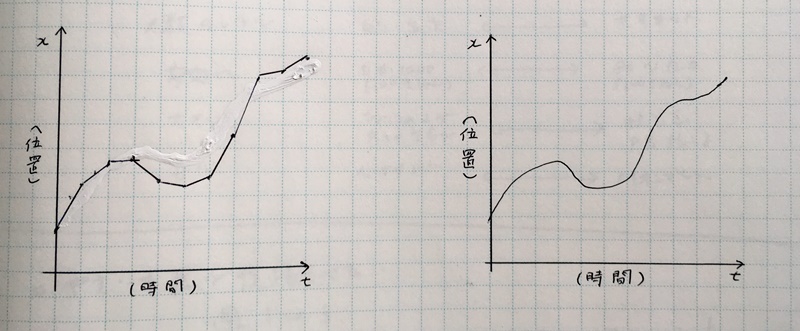
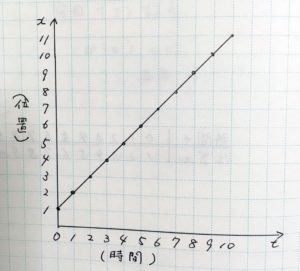
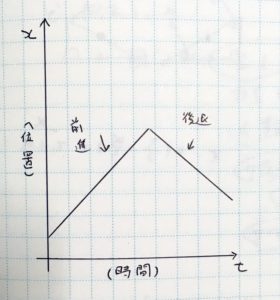
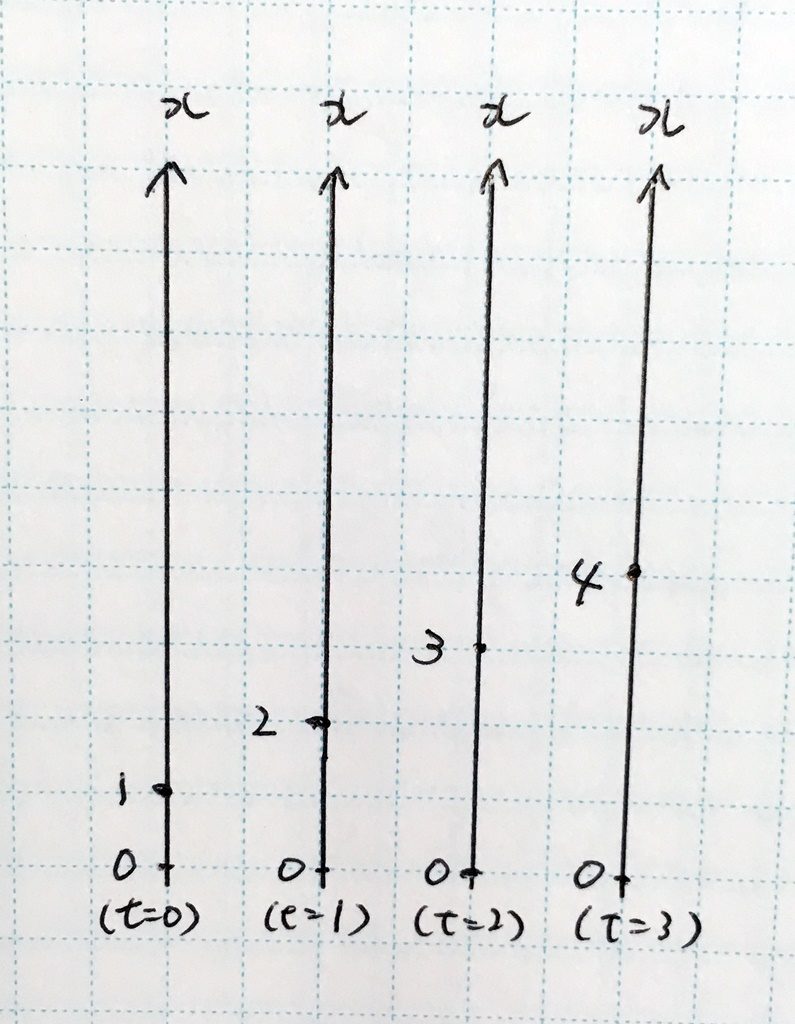
まずは前回、てちこ画伯に書いてもらったグラフを振り返りたいと思います
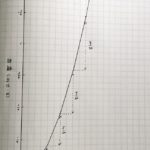

へー、これてちこが書いたんだ

うん

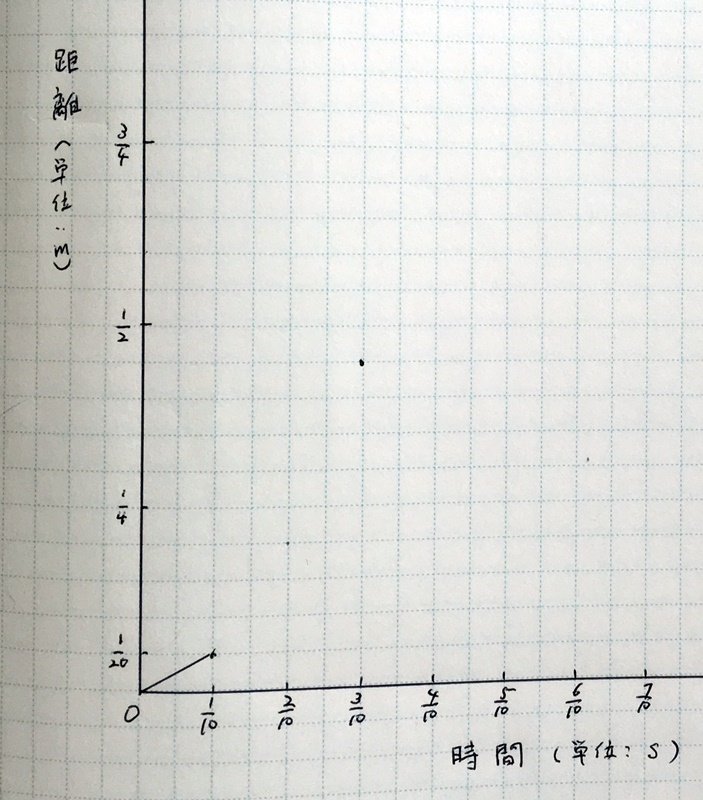
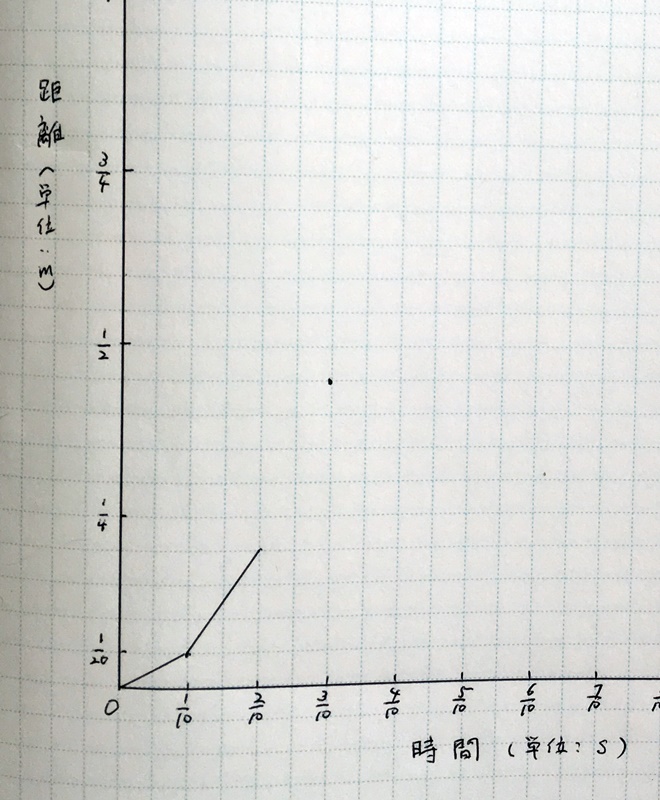
前回書いたグラフでは1秒を10分割したことにしたけど……
時間を1秒っていう具体的な量じゃなくてtっていう抽象的な量に置き換えて、分割する数も10じゃなくてnにした方が後々考えやすくなるから、そうするね。

はい
ではtをnで分割した微小な時間はどう表せる?

え? どういうことですか?

$$時間tをnで割った、\frac{t}{n}だよ$$

正解!

すごい!

えっへん

それで、これも前回出てきた量ですが……
$$加速度b = nw を変形して、w = \frac{b}{n} にします。$$

wというのは速さの変化量でした

はい
$$これは、”b かける \frac{1}{n}” ということを表しているんだけど、$$
$$\frac{1}{n}の”1″は何のことかわかる?$$

えーと、1秒ですかね

そうです。
では1秒じゃなくて、時間をtという文字であらわすことにするとどうなるかな

$$w = \frac{bt}{n}$$

ナイスセゾン!

てちこ凄い

ふふふ、なんで私の時はナイスセゾン!なんですか(笑)
では、この式を使って、速さvの時間変化を出していきたいと思います。もう一度言うと、wというのは速さの変化量です。

はい
$$時刻0では速さv_{0}は0でした。$$
$$そこからある一定の短い時間t_{1}を過ぎた後の速さを$$
$$v_{1}で表すとして、v_{1}はwを使ってどう表せる?$$

えーと、$$v_{1}=w$$

そうです。
$$じゃ、そのあとまた時間t_{1}が過ぎた後の速さをv_{2}で表すとすると、$$
$$v_{2}はどうなるかな$$

$$v_{2}=v_{1}+wです$$

$$v_{1}=wだったから、v_{1}に代入してみようか$$

$$v_{2}=w+w=2w$$

じゃあ……
$$さらにまた時間t_{1}が過ぎた後の速さをv_{3}で表すとすると$$

$$v_{3}=v_{2}+w=2w+w=3w$$

すごいじゃん

え? そんなに難しくないよ

丁寧にやってるからね。
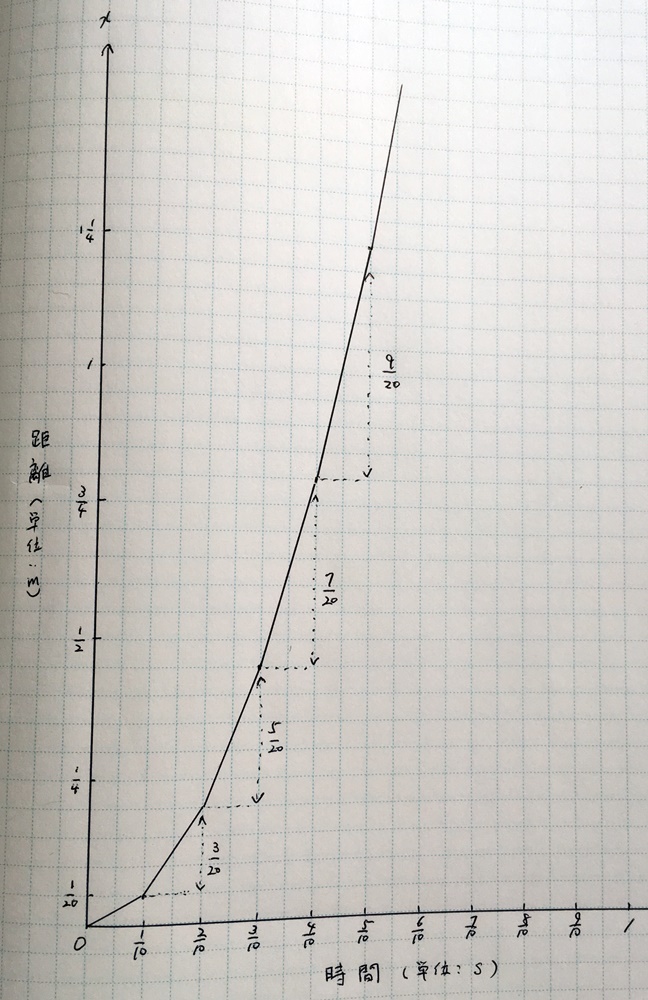
で、今度はジェットコースターのどれだけ移動していったか、xについて調べていきたいと思います

こんどは位置ですか……

そう、最終的に知りたいのは位置になるからね。
ジェットコースターのレールに沿って、xの軸を決めよう。

ジェットコースターの話になってるんだ

そうなんだよ。で、尾関が乗ってるの、リアクションチェックの時の話。

えー、それ黒歴史だよ(笑)

じゃあいくよ
$$時刻0では位置x_{0}は0でした。$$
$$そこから短い時間t_{1}を過ぎたときのジェットコースターの位置をx_{1}とします。$$
$$この時間t_{1}の間は、$$
$$ジェットコースターは速さv_{1}という一定の速さで動いたということにして、$$
$$x_{1}はv_{1}とt_{1}を使ってどう表せるかな?$$

えーと、掛け算すればいいですよね。$$x_{1}=v_{1}t_{1}$$

正解。
$$ところで、ここから先、短い時間をt_{1}で表すのはやめて、$$
$$さっき出てきた\frac{t}{n}だった、という事にするよ。$$

オー、正体ヲ現シマシタカ! 一般化トイウヤツデスネ

え? 何?

ワタシハ、オゼ・クリン・リキャ

急にキャラが変わった(笑)

あ……ありがとうございます。リキャ捜査官、お疲れ様ですが、もう結構です

おーい、せっかく盛り上げようと思ったのに!

(笑)突然過ぎなんだって
話を元に戻すと、$$x_{1}=v_{1}t_{1}に、t_{1}=\frac{t}{n}を代入して$$

$$x_{1}=v_{1}\frac{t}{n}デス$$

まだオゼ・クリンやってる(笑)

さすがです
$$じゃあさらに時間\frac{t}{n}を過ぎたときの位置x_{2}は?$$

マッカセナサイ
$$x_{2}=x_{1}+v_{2}\frac{t}{n}=v_{1}\frac{t}{n}+v_{2}\frac{t}{n}=\frac{(v_{1}+v_{2})t}{n}デス$$

その通り
$$二番目の時間区間では、ジェットコースターはv_{2}という速さで進んだと仮定するんだね。$$
$$では同じようにして、さらに時間\frac{t}{n}過ぎたときの位置x_{3}は?$$

$$x_{3}=x_{2}+v_{3}\frac{t}{n}=(v_{1}+v_{2}+v_{3})\frac{t}{n}$$デス

すごい。さすがリキャ捜査官

ィエーィ

んフフ(笑)

では、さらに時間がたって
$$n番目の時間区間になったらx_{n}はどうなりますか$$

リキャ捜査官?

$$x_{n}=\frac{(v_{1}+v_{2}+v_{3}+…+v_{n})t}{n}$$デスネ

素晴らしい。ところで
$$さっき、v_{1},v_{2},v_{3}というのはそれぞれwを使って表せて、$$
$$v_{1}=w, v_{2}=2w, v_{3}=3wになるという話をしました。$$

これを上の式に代入してみると

$$x_{n}=\frac{(w+2w+3w+…+nw)t}{n}$$ $$=\frac{(1+2+3+…+n)wt}{n}$$ デスヨ~

この$$1+2+3+…+n$$は簡単になるってわかる?
こ

$$1+2+3+…+n = \frac{(1+n)n}{2} $$デスネ

え? すごい!

さすがです。なんでそうなるか説明できる?

ハイ……あの、その前に、ちょっと普通に話していいですか? なんか疲れちゃって

(笑)おかしい!

(笑)普通でいいよ

はい、では改めまして。
これは、$$1+2+3+…+n$$というのを二つ用意するんですけど、片方は数字を書く順番を逆にして、$$n+…+3+2+1$$って書くんです。
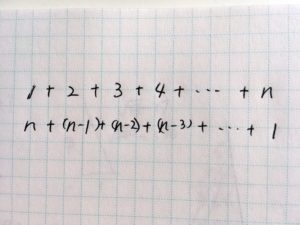

ふんふん

で、これを二行並べて書いて、上と下を足し算します


ふーん

そうすると、”1+n”っていうのが、何個も並ぶのね

なるほど……

では、何個並ぶでしょうか、てちこわかる?

え? 何個だろう?

1,2って数えてnまであるから、n個だね
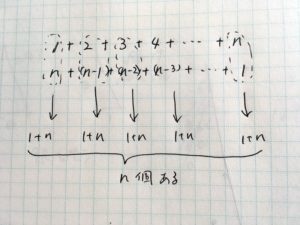

そうです。”1+n”がn個並ぶことになります。なので、この足し算の答えは(1+n)nです

おー

ところで、元に戻ると、今やってたのは$$1+2+3+…+n$$という計算を二回やったことになります

うん、そうだね

だから、1+2+3+…+nという計算の答えは、(1+n)nを2で割った$$\frac{(1+n)n}{2}$$です
$$1+2+3+…+n=\frac{(1+n)n}{2}$$

お見事です

おぜすごいね

では、ここからさらに……と行きたいところだけど、結構長くなったのでこの続きは次回にしたいと思う!

はあ、長かった。では、生徒の皆さんとはまた次回お会いしましょう

おぜちゃんは次回も登校お願いするね

はーい