ここからの時間は、ゆーき先生が欅坂46平手友梨奈ちゃんをイメージした架空のキャラクターてちこちゃんに相対性理論を教える教室。前回のてちこちゃんはなかなか冴えているとゆーき先生から褒められてていたが、今回もこの調子で頑張ってほしい! では早速ゆーき先生の相対LOCKS!

生徒の皆さんこんばんは、相対LOCKS担当のてちこです。前回は、次元って話をしましたね。そういえば、ルパン三世ってアニメがあるじゃないですか。あれに出てくる帽子をかぶった人って確か次元でしたよね。関係あるのかな
ガラガラ(扉の開く音)

関係ありません

わっ、ゆーき先生こんばんは

てちこ君はルパン三世も見ていたのかね

子供のころ、再放送とか、たまに映画みたいのやってましたよね

じゃ、不二子のまねやって。『ルパーン』ってやつ

絶対いや! それよりも今日は何の話ですかっ?

今回も前回に引き続き、直線運動について、もうすこし色々なパターンをやります

はーい

前回は、欅坂46の4thシングル『不協和音』のカップリング曲『エキセントリック』のミュージックビデオから、平手友梨奈ちゃんが歩いているシーンを題材に、直線運動の様子を表にしたり、グラフにしたりしました
復習したい人はここをクリック!

はい、そうでしたね

ちなみに『不協和音』のシングルは初回限定版としてType-A、B、C、Dの四種類に加えて通常版というのがあり、『エキセントリック』はこの通常版にのみ収録されている! それから、欅坂46の1stアルバム『真っ白なものは汚したくなる』にも収録されているからチェックするように!

え、なんかここ宣伝ぽく無いですか?

良いんだよ! 欅坂46の楽曲が売れてくれれば!

ふふふ、ありがとうございまーす

話を戻すと、前回は平手友梨奈ちゃんは時速3.6kmで歩いていると仮定して表やグラフを書きました。
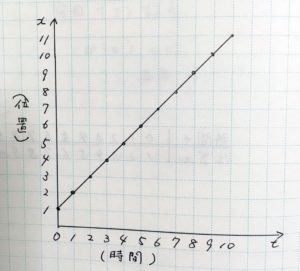

それで、友梨奈ちゃんが歩く速さを実際に近い、時速5.4kmに仮定してグラフを書くとどうなると思う?

えーと、傾きが急になりますかね?

そう、グラフのt軸に対する傾きが大きくなります。それをグラフにしたのがこちら
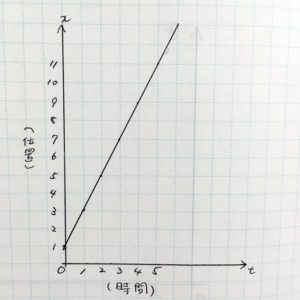

はい。正解でーす、やった

じゃあ、この図はどんな運動だと思う?
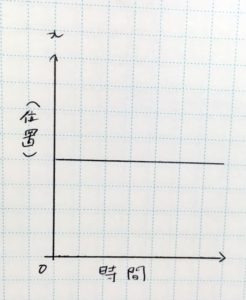

あれ? 今度は線が真横になってますね

t軸、つまり時間軸に平行ね。これは一か所に止まっている場合になります

なるほど……。じゃあこの次のグラフは何ですか? 急に折れ曲がってます
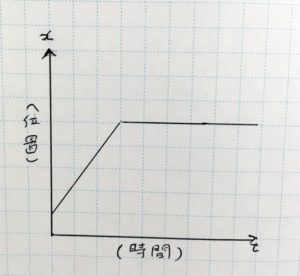

これについては、こちらの動画をご覧ください

あっ、セゾン、二人セゾンだ!

そう、二人セゾンのミュージックビデオ。サビの部分で、みんなが歩いて、途中で止まってクルッってした

振り返りました

つまり、グラフのこの部分までは歩いていて、ここで止まって振りむいたということになる


ナイスセゾン

おいおい。じゃあこれはミュージックビデオにはないけど、振り返って逆方向に歩きだしたらどういうグラフになると思う?

えーと、こうですかね?
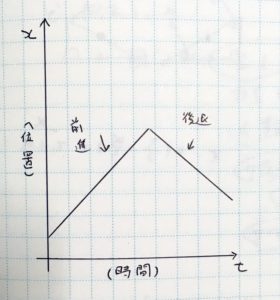

ナイスセゾン! その通りです

あ、まねした。ナイスセゾン

ふたりセゾーン

(笑)

じゃ、もうちょっとやるよ。二人セゾンのミュージックビデオ(1:18から)で、ゆいちゃんずの二人が歩道橋の上で突然鞄を投げ出して、歩きながら踊る、そのあと一瞬立ち止まって小林由依ちゃんが振り向き今泉佑唯ちゃんを見て駆け出した。これをグラフにするとこんな感じだ
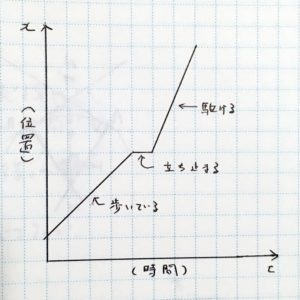

ずいぶんカクカクしますね

急に立ち止まったり、駆け出したりするとこうなるね。で、ここからはミュージックビデオから離れるけど、もっと短い時間で細かい動きの変化があるとすると、グラフはだんだん滑らかな曲線になっていく
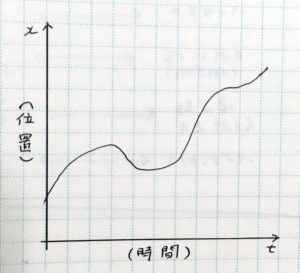

はい

それで、これは何が起きているかというと速度が連続的に変化する運動、言い換えると加速運動または減速運動がおきているといえる

ふーん

で、この加速や減速というのがどういう感じで起きているのか、というのを厳密に調べていこうとすると、微分というものを知らないといけないんだけど

びぶん? なんですかそれ?

微分は数学IIIでやる内容だから、高2のてちこは知らなくてもいいよ。この教室では、滑らかな線を細かくみて、短い時間の間隔では等速運動をしていると仮定して、つまり滑らかな線を細かい折れ線に置き換えて考えてみる

はい、それでどうなるんでしょう?

この先はまた次回にしたいと思います

えーっ、なんか先が知りたいような、でもちょっとほっとする……

次回をお楽しみに! では今日の相対LOCKSは以上

生徒の皆さんとはまた次回お会いしましょう
