ここからの時間は、ゆーき先生が欅坂46平手友梨奈ちゃんをイメージした架空のキャラクターてちこちゃんに相対性理論を教える教室。前回はなんとゆーき先生がてちこちゃんをじらす作戦、今回の教室でてちこちゃんはモヤモヤを解消できたのか? では早速ゆーき先生の相対LOCKS!

生徒の皆さんこんばんは、相対LOCKS担当のてちこです。前回は、二人セゾンの話から、ビブン? なんか難しい数学の話になりそうな感じでした。それで、私はまだ高2だからそれは知らなくていいっていう話で……
ガラガラ(扉の開く音)

おーよく憶えていてくれました

あ、二回連続ほめられた、やった

でもまずは挨拶だね

こんにちは先生

こんにちは、今日もよろしくね

(笑)なんすか、改まった感じで

いや、これが素だから。じゃあね、今日は前回の続きから始めたいと思います

はい
これは前回にも出した図だけど、滑らかな曲線を細かく見て、折れ線グラフになっていると考えよう。それがこの図です。
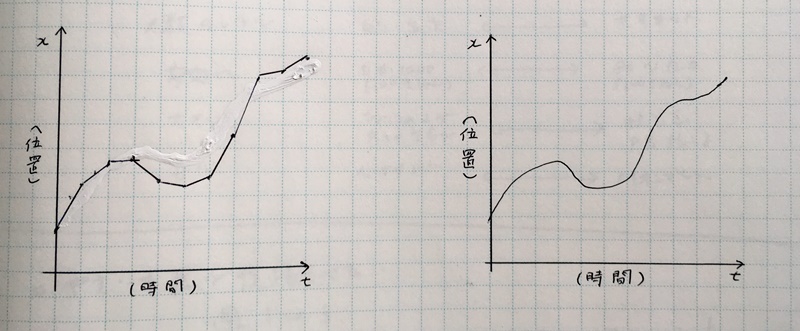

カクカクしてますね

それで、この折れ曲がっている点、つまり頂点と隣の頂点の間は、時間的には等しいと仮定する

どういうことですか?
二つのグラフは方眼紙に書いてあるけど、方眼紙の縦の線、これは時間の線だけど、この線と線の間隔はどこをとっても同じという事ね

なるほど
で、この時間の間隔は、1秒をnという数で割った時間、
$$式で表すと\frac{1}{n}秒ということにします$$

急にnって出てきましたね
nはよく自然数の意味で使うよ。2とか、100とか、5000とかね、何でもいいんだけど『なんか大きい数』という事にしておこう

なんか、あいまいだなあ

あんまり具体的な数にはしたくないんだよ。で、もう一つ仮定することがあるんだけど

はい、何でしょう?
$$この、\frac{1}{n}秒間は、平手は一定の速度で歩いています$$

あ、はい。って急に平手って名前が出てきてびっくりしました

そうそう、一応『二人セゾン』から続いてるからね

あ、そうでした(笑)

ナイスセゾン。それで、ここで二人セゾンの話から離れます

はい……

突然だけど、「欅って、書けない?」でやった「初めてのリアクションチェック」って憶えてる?

憶えてますよ! お化け屋敷が超怖かったです
そうそう、ただ、いま取り上げるのは戦慄迷宮じゃなくて、FUJIYAMAの方ね

あ、尾関梨香って子が……

いや、そこから後はもう言わなくていいです(笑)
ジェットコースターって、一旦高いところ行って、そっからダーッと落ちるじゃない。

落ちますね
ああいう運動のことを今から考えます。一番高いところから落ちるときって、最初はゆっくりでだんだん速くなるよね。

そういえば、そうですね
$$\frac{1}{n}秒ごとに落ちる速さが変わるとして、$$
$$その変化量をwという文字であらわすとするよ$$

はい
この速さの変化が1秒間続いたとして、1秒間の速さの変化の合計はどうなるかな

1秒間にn回変化したことになるんですよね。だから、nとwをかけてnwです

ナイスセゾン!

やった、正解でーす
このnwであらわされる量をbという文字であらわすことにしよう。$$式で書くと nw = b ね$$

急にbって出てきましたね

出会いはいつも突然なんだよ
で、このbは『加速度』って言うんだけど、この加速度がどの時間区間でも同じ場合に、『この運動は等加速度運動だ』って言うのね

そうなんですか

ま、これは言葉だけの話だから、憶えてくださいな

はーい

それじゃあ、これから一つ例を出すよ
時刻0秒の時点で、ジェットコースターはx=0メートルの位置にあって、これから落ちていきます。
いままで話したように、細かく時間を見ていきたいので、
$$n=10、つまり\frac{1}{10}秒という単位で、$$
時間の間隔を刻んでいきます

はい……
それと最初の時間区間、つまり
$$t=0からt=\frac{1}{10}のあいだ、$$
$$ジェットコースターは秒速\frac{1}{2}メートルで進む、$$
ということにします。

はい……大丈夫かな

では問題
$$t=\frac{1}{10}の時点で、ジェットコースターは$$
$$x=0からどれくらい進んだことになるでしょうか?$$

えーと
$$\rm{速さの\frac{1}{2}[m/s]と時間\frac{1}{10}[s]をかけて、\frac{1}{20}[m]ですか?}$$

ナイスセゾン。図に書くとこうなる
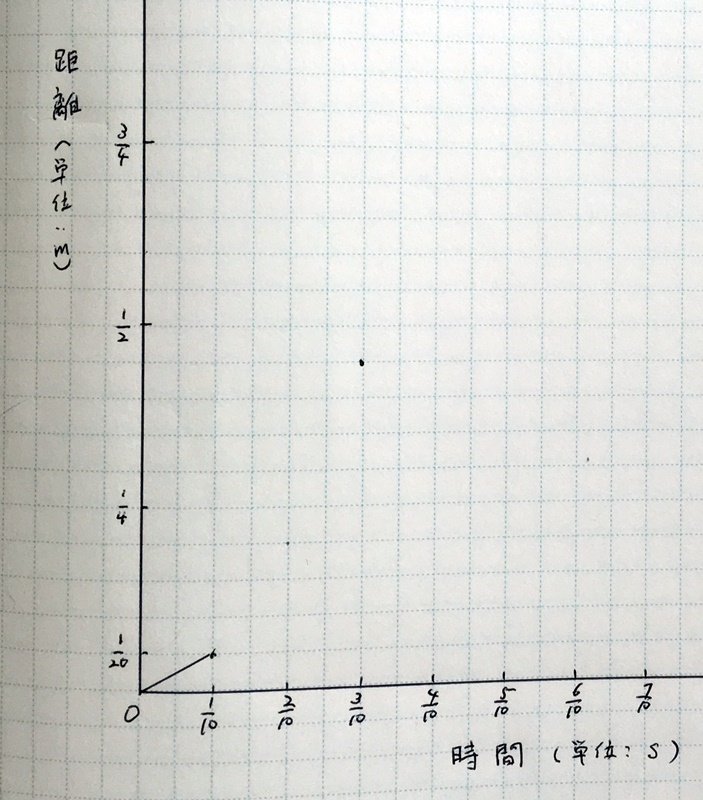

はー、よかった

では次にいくよ
$$ジェットコースターは時刻\frac{1}{10}から時刻\frac{2}{10}のあいだは$$
$$秒速\frac{3}{2}メートルで進むとします。$$

この場合、速さの変化量wはどうなっている?

え? え? もうわけわからない!

おちついて。wは速さの変化だったよね、
$$一つ前の時間区間(0~\frac{1}{10})と、今の時間区間(\frac{1}{10}~\frac{1}{20})で$$
速さがどれくらい変わったかを調べればいいんだ。

どう調べるかというと、引き算をすればいい

引き算。えーと
$$\rm{\frac{3}{2}[m/s] – \frac{1}{2}[m/s] = 1[m/s]ですか?}$$

ナイスセゾン
$$では、ジェットコースターは時刻\frac{2}{10}の時点で、$$
どの位置にいるでしょうか?

えーと、式にするとどうなるかな……

さっきのグラフに書くとわかりやすいかもよ

そっか、スタート地点がわかりますね。ここからこう線をひっぱって……はい
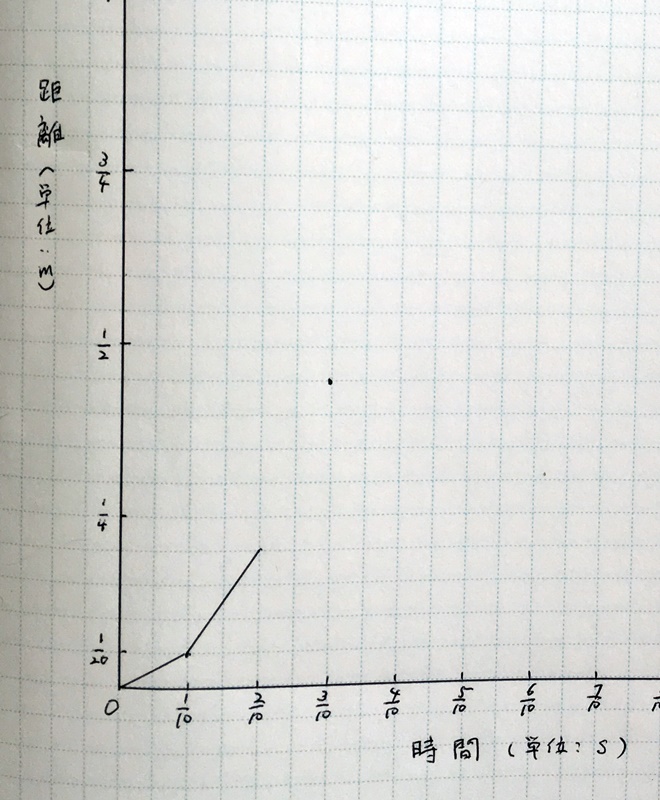

さすが! てちこ画伯

ふふふ、ただ線を引いただけですよ

この調子で時刻10分の5秒まで書いてくと、グラフはこんな感じになる
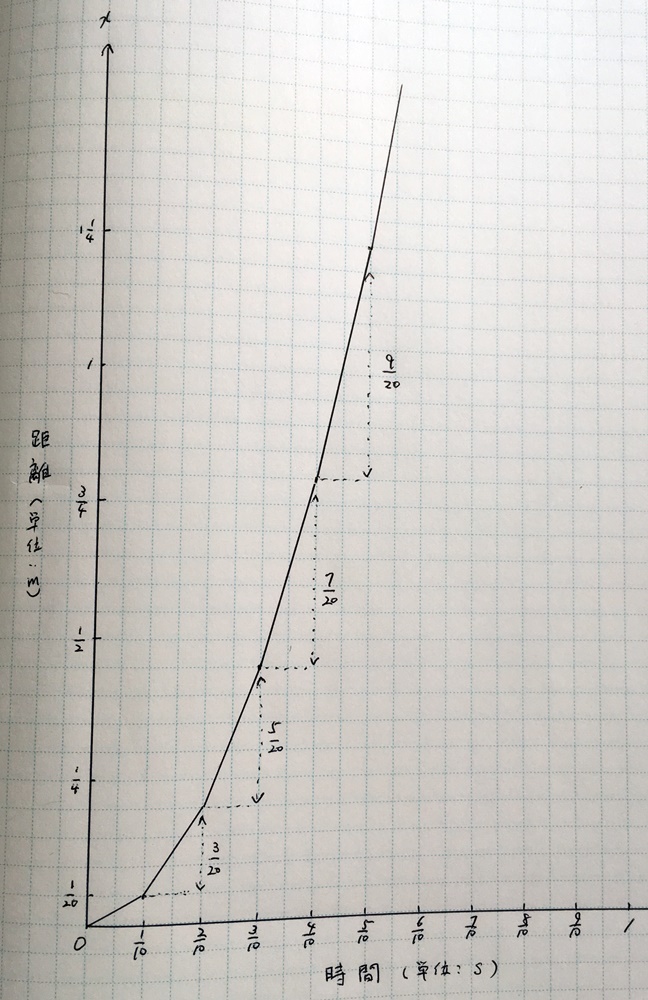

はい
さて、ここで、改めて、wとbについて考えてみよう

え? あー、えっとb、bですよb

$$b = nw$$だったよね

はいっ、そんな感じ、だったと思います!

元気でよろしい
$$nというのは「時間を何分割したか」という量です$$

いま書いたグラフでは何分割でしたか?

10分割でした

ナイスセゾン。それで、nという量の次元は、時間の次元Tの逆数になります。
$$nの次元は\rm{ [\frac{1}{T}]または、[T^{-1}]}になる$$

はい

では、bの単位はどうなりますか?

はい、えーと、$$b = nw$$ で……
$$nの次元は\rm{[\frac{1}{T}]}で
wの次元は\rm{[\frac{L}{T}]だから[\frac{L}{T^{2}}]}ですね。$$

はい、正解、ナイスセゾンです!

ナイスセゾン! 今日はセゾンばっかりですね

この話はさらに続くんだけど、今日は長くなったのでこれで終わりにします

はい。では、生徒の皆さんとはまた次回お会いしましょう。(ふーやっと終わったよ)
