ここからの時間は、ゆーき先生が欅坂46平手友梨奈ちゃんをイメージした架空のキャラクターてちこちゃんに相対性理論を教える教室。だんだん物理っぽい話になってきた気がするが、ついていけてるだろうか?
では早速ゆーき先生の相対LOCKS!

生徒の皆さんこんばんは、相対LOCKS担当のてちこです。前回は、いや前回も、か。なんか突然終わった気がしたんですが
ガラガラ(扉の開く音)

そんなことないぞ!

こんばんは先生。前回は運動って何ってところで終わりました

おっ、素晴らしいちゃんと憶えてる

ふふふ、これでもちゃんと聞いてるんですよ

よしっ! では今日も始めていくよ!
今日は前回の続きで、運動についてなんだけど、まずこの『運動』というのを物理の言葉で説明できないといけないね。

そう、なんですか

前回てちこちゃんが言ってくれた『ガタッ』とか『ビヨーン』では物理の言葉とは言えない

あ……まあそっすね

なんか急にやる気そがれた感じの返事だな。続けるけど、この物理の言葉というのは、数式で表すことが本来だけれども、数式はどうだ?

えーっと、まあ、あんまり……苦手ですね

と、いうわけで、今回の授業では、はじめは数式ではなく、表やグラフを使って説明したいと思う

それならわかるかもしれません

あ、1+1=2 レベルの簡単な式は出てくるからね。そんなに怖がらないでね

大丈夫かな……

まずはじめに、一番簡単な、直線状の点の運動について書いてみる
突然だけど『エキセントリック』のミュージックビデオで3分01秒あたりから平手友梨奈ちゃんは道を歩いてたよな

はい、左足は裸足でした
実際のミュージックビデオでは多少左右に揺れながら歩いてるけど、あれをまっすぐ一直線に歩いてたということにしよう。

友梨奈ちゃんは結構速足だったのかな

そうですね、多分普通の人よりは速いと思います

途中で走ったりとか、いきなり立ち止まったりとかしてないよね

はい、ビデオではしてませんね

では、エキセントリックのミュージックビデオの中で、欅坂46平手友梨奈は一直線に歩いていた、ということにしよう
3分01秒の時点を、時間の原点、$$t=0$$とおいて、平手は原点から1メートル離れたところにいるとする。

これは今回表を作るためにそういう風に決めた

はい
平手友梨奈が歩いていた方向をx軸にする。1秒後には原点から2メートル離れた地点に平手は歩いて移動した

これって速いんですか?

実際よりもかなり遅いと思うけど、計算しやすいからこうするよ。
続けて、2秒後には3メートル離れた地点に平手は移動した

はい
こういう風にして、3秒後、4秒後と、時間t秒と進んだ距離xメートルの関係を表にまとめてみた
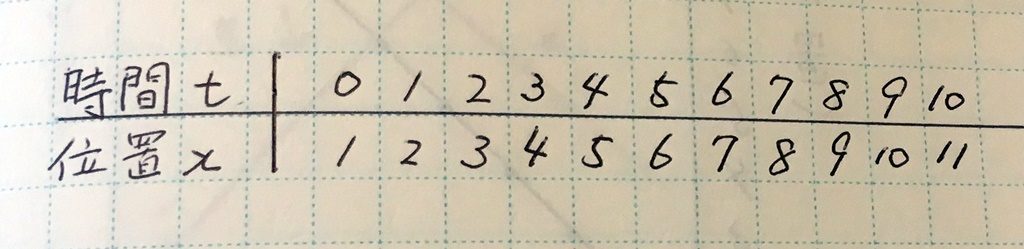

なるほど……
また、時刻t=0の平手の位置x、t=1の平手の位置、という風に、各時刻での平手の位置を表したグラフを作って、左から右に横に並べてみたのがこれだ。
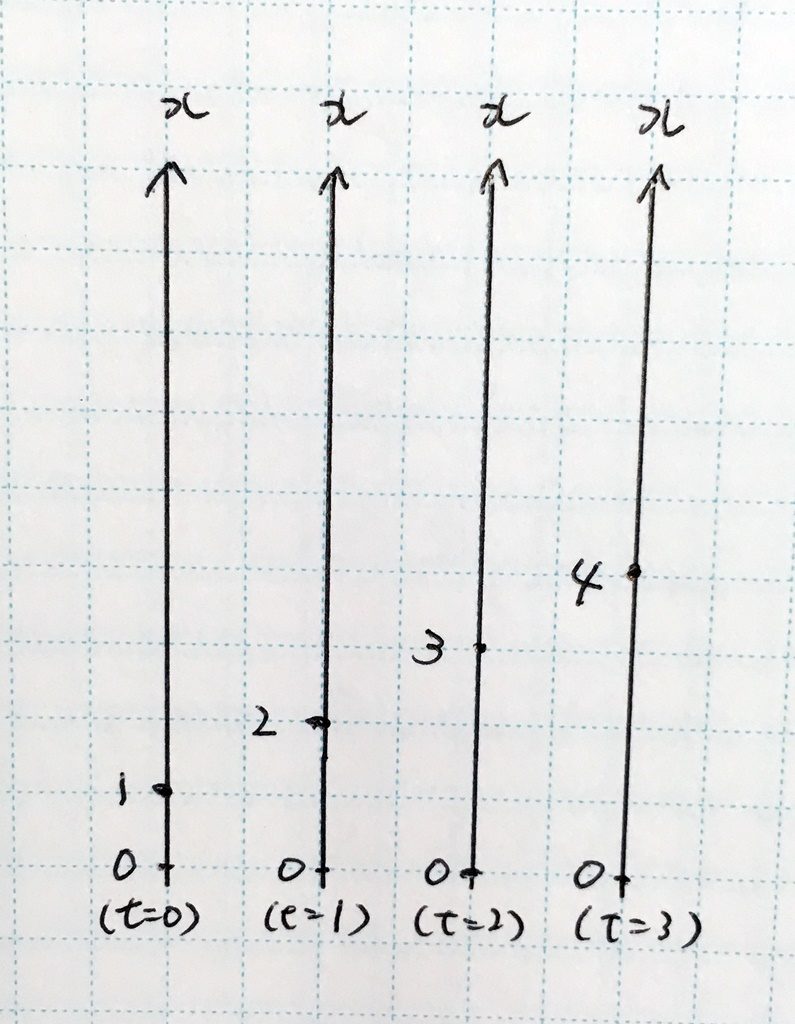

ちょっと不自然に思うかもしれないけど、縦軸が位置ね

点が斜めに並びますね
それで、この横に並べたグラフを、横軸を時間t、縦軸を原点からの距離xという、縦横2つの軸のグラフにする
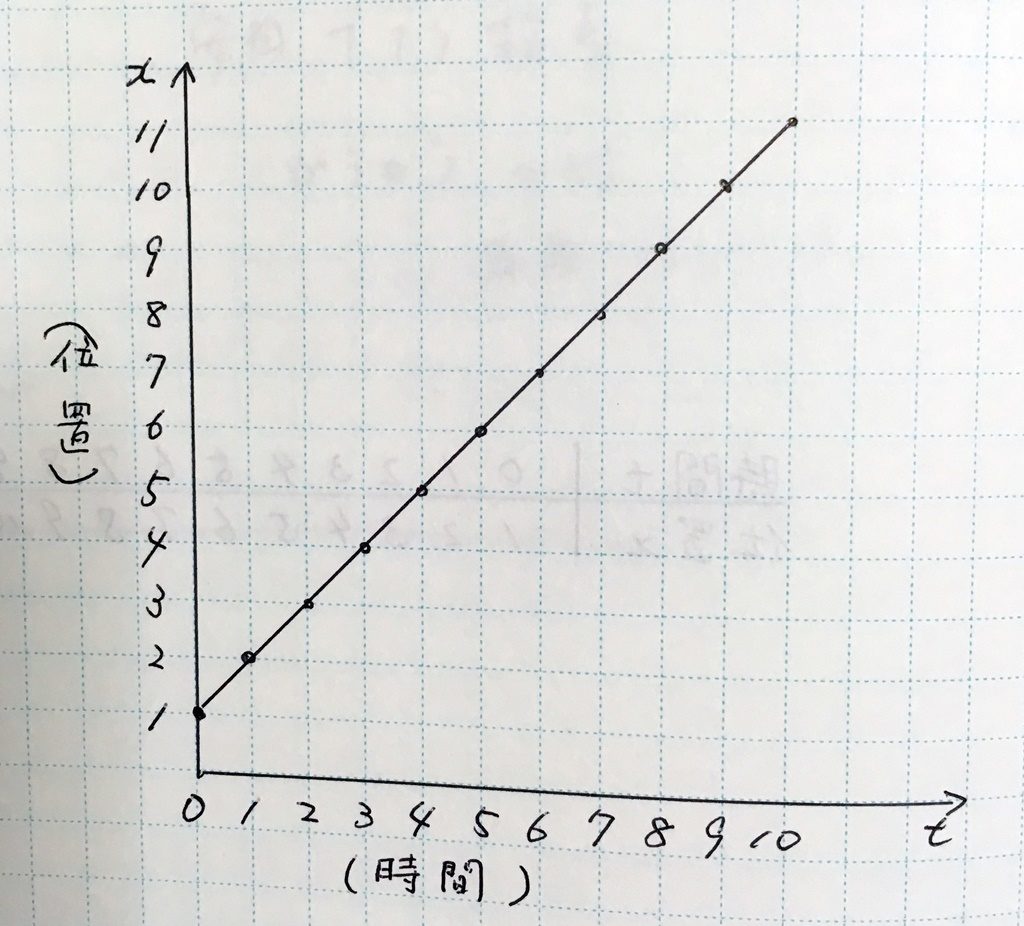

するとこうなるのはわかるよな

はい、各時刻での位置の点を、斜めの直線で結びました

このときの、グラフの傾きってわかるか? 黒板に書いてみて

え? 傾き? えーっと。はい、こうですかね
$$\frac{x}{t}$$

正解! 素晴らしい

やったー、正解です

はい。いま書いたような運動は「等速運動」(または「一様な運動」)という
ここで、時間と進んだ距離の比を「速さ」と決めて、記号vで表すことにすると、vは次の式で書ける
$$v=\frac{x}{t}$$

さっき書いたグラフの傾きですね

そうなるね
この式から、速度の単位は簡単にわかる。それは1秒間に1メートル進むような速度になる。これは組立単位と呼ばれるものだが、特に新しい名前は付けずに、m/s(メートル毎秒)で表すことにする。

『秒速なんとかメートル』っていうのと同じことですか?

きょうのてちこは冴えてるな! そう、同じです

ふふふ、それほどでも
それで、この$$v=\frac{x}{t}$$という式に対応して、『速度は距離を時間で割った物理的次元を持つ』という言い方をすることもある。これを数式でこう書く
$${\rm [V]=[\frac{L}{T}]、または[V]=[L,T^{-1}]}$$

この[](四角いかっこ)とか、LとかTとか、あと$$^{-1}$$って何ですか?

先に-1について説明するね。分数の分母を表す場合、べき乗の数字にはマイナスの記号「-」をつけて表す。つまり$${\rm T^{-1}は、\frac{1}{T} と同じ}$$

うーん、はい
それからLとTのことだけど、LもTも『次元』を表す記号だ。Lは長さまたは距離を表す次元、Tは時間を表す次元のことだ。それで、四角いかっこ [ と ] は、「これは次元の計算式です」というのをハッキリさせるためにつける

んー、わかったようなわからないような……これ何の役に立つんですか?

物理は数学と違って、数字で表される量には必ず次元というのがある
この次元が決まると、単位が決まる。それから、複雑な計算をした後にこの次元をチェックして、未知の量にどんな物理的な意味があるかを推測するヒントにしたり、この次元がおかしい場合は計算が間違っているという判断にもなるんだ

よくわかりません

てちこ君は正直でよろしい! あとで忘れた頃に出てくるかもしれないから、そんときに思い出してくれればいい

はーい

最後にちょっとお知らせ


さて、脇道がちょっと長くなったので、続きは次回にしよう。というわけで今回は以上!

では、生徒の皆さんとはまた次回お会いしましょう
